Filippov systems are dynamical systems with discontinuities. They are being used to model the dynamics in cases where there is very rapid transition between different dynamical regimes. For example, if in a predator-prey system the number of prey crosses a threshold then the predation rate can increase discontinuously.
As the simplest case of a Filippov system one can consider a two-dimensional dynamical system where the phase space is separated into two regions. A smooth dynamical system is defined in each region but the two systems do not match in a continuous way along the discontinuity boundary.
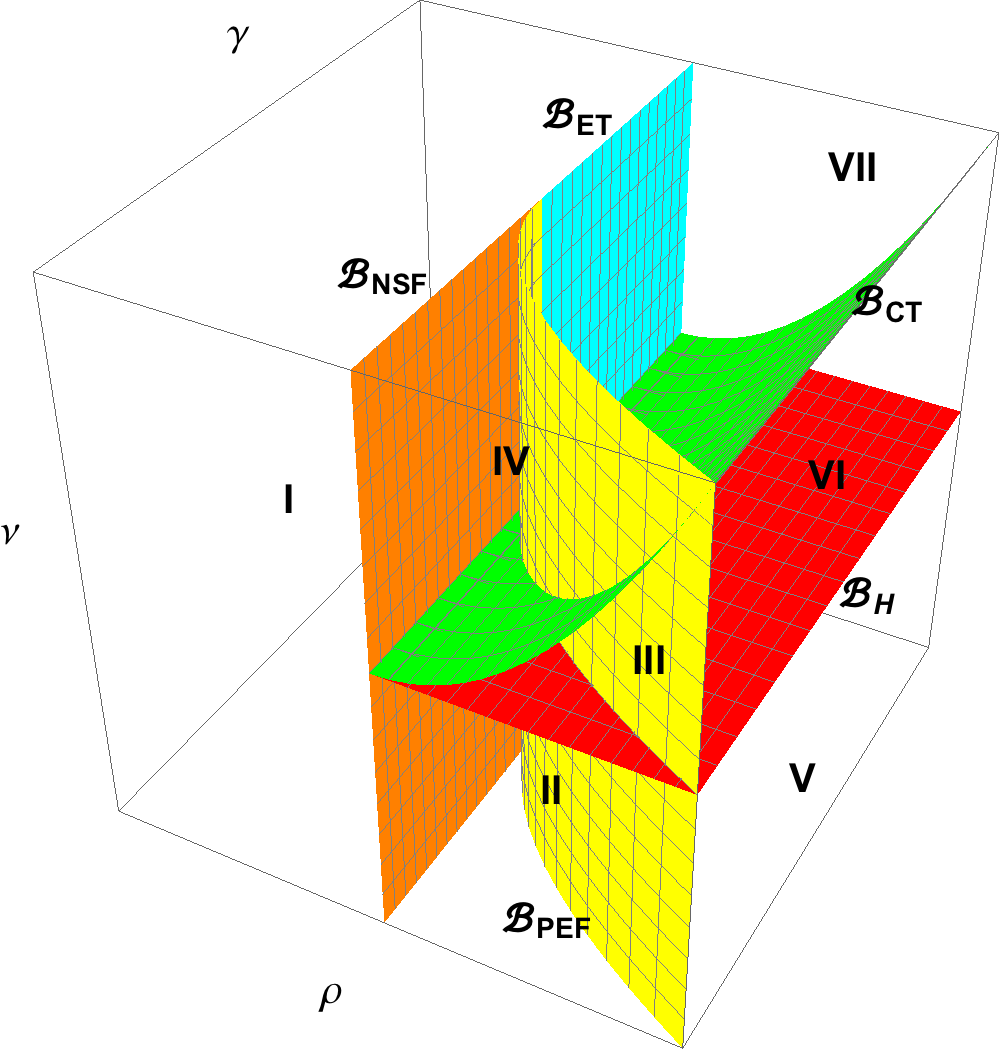
The interaction of the two vector fields at the discontinuity boundary induces bifurcations that are not found in smooth dynamical systems. Such discontinuity-induced bifurcations are organized in families often also containing smooth bifurcations. One particularly interesting case is when one of the two smooth dynamical systems making up the Filippov system undergoes a Hopf bifurcation (a typical mechanism for the creation of instability and limit cycles in smooth systems). The dynamical system at the other side of the discontinuity boundary is assumed to be transversal to the boundary but at a special position so that the Filippov system goes through a boundary-fold bifurcation.
In our recent work with Xia Liu and Henk Broer we studied the bifurcation diagram in the neighborhood of such Boundary-Hopf-Fold points. We derived a local normal form for such systems and determined the 8 possible local bifurcation diagrams thus completely classifying the dynamical behavior near Boundary-Hopf-Fold points. One of these diagrams is shown in the picture above. We finally applied our results to a population dynamics model and compared our theoretical analysis to numerically obtained results. The paper has been published at the SIAM Journal of Applied Dynamical Systems.